附录一 何谓复利#
累积财富,不在开源节流,
而是以钱赚钱的复利力。
爱因斯坦被誉为历史上最伟大的科学家,曾有人问他:“世界上最强大的力量是什么?”他的答案不是星球挤压的力量或核子爆炸的威力,而是“复利”(Compounding)。
由前例所言,到底是什么因素,能够让每年存的1.4万元,40年后增长为1亿多元,答案是“复利”。既然复利是促使我们财富加速成长的主要因素,因此想要利用理财致富,首先必须对复利有所认识。
假设你在求职时,有两个工作机会可供选择,第一份工作是月领10万元,另一份工作则是第一个月的薪水为1元,但以后每个月的薪水是上一个月的2倍。假设这两份工作的工作时间皆为两年(24个月),试问你会选择哪一份工作?
乍看之下,似乎第一个工作较佳,每个月领10万元,24个月后的总收入是240万元;但若了解“复利”作用的人,一定会选择第二个工作,因为第二个工作在24个月后,总收入为1677万余元!这就是复利所产生的效果。当然这是极端的例子,现实生活中不太可能出现以如此高比率增长的情况。但从这个简单的例子中,复利的威力已展露无遗。
相信每个人对于复利都略知一二。至少你应该知道,将钱存在银行,长期后便能产生复利效果,这似乎已成为现代人所应具备的基本常识。“复利”既然被爱因斯坦尊为世上最强大的力量,而且也将是带领我们,以小钱便能跻身亿万富豪的凭借,身为现代社会中的一分子,尤其是想学会投资理财的人,应该对“复利作用”有更深一层的认识。
复利,简言之就是利滚利。一般人都知道钱存银行可以赚取利息,且银行存款利息亦采用复利的方式计算。兹举一例说明,假设银行利率10%,今天存入1000元,1年后可赚得利息100元,即本利和为1100元。这1100元如果继续存在银行,两年后的本利和为1210元,第2年赚得的利息为110元,依此类推,第3年的本利和为1331元,赚得的利息为121元。
值得注意的是,第三年的利息高于第二年的利息,第二年的利息高于第一年的利息。第三年的利息何以较第二年的利息高?第二年的利息何以高于第一年的利息?原因是第一年所产生的利息于第二年可以再生利息,同样地,第二年所累积的利息于第三年又可再生利息,使利息越滚越多。这种“利滚利”的情形,就是复利。
由下表可看出,第26年后,每年所赚得的利息已超过本金,而第40年所赚的利息4114元,是原始本金1000元的4倍多。
1000元在利率10%的复利作用下之未来值
| 年 | 年初值 | 年底值 | 利息 |
|---|---|---|---|
| 1 | 1000 | 1100 | 100 |
| 2 | 1100 | 1210 | 110 |
| 3 | 1210 | 1331 | 121 |
| … | … | … | … |
| 26 | 10835 | 11918 | 1083 |
| … | … | … | … |
| 39 | 37404 | 41145 | 3740 |
| 40 | 41145 | 45259 | 4114 |
在各种不同利率以及不同时间(年数)之下,复利会产生不同的效果。以此列出的表称为复利表(参阅本附录)。复利表是由利率、年数及终值利率因子(即由公式所计算出增长的倍数)所构成,成堆的数字令人望而却步。但我邀请阁下仔细端详,因为学会看懂复利表,对投资理财极有帮助,你会发现它是无价之宝。复利表被美国著名的理财顾问范卡斯佩尊为“世界第八大奇迹”,阁下若没有机会出国观赏世界奇观,或可仔细观察此表。最重要的,若想利用复利创造奇迹,利用小钱成为亿万富翁,对于复利的特征应有所了解。
由复利表中,读者不难发现,表中的数据随时间及利率大小渐增,但是光知道这点是不够的,复利究竟还具有哪些特性呢?读者在观看由复利表所形成的复利图像,便可豁然大悟。图1-1的假设条件为:每年年底存入1元,在不同的利率下,10年中总资产的增长趋线;图1-2的基本条件同图1-1,所不同的是,将时间由10年拉长为40年。

图1-1:不同利率、期数下,1元之年金未来值增长图(10年)
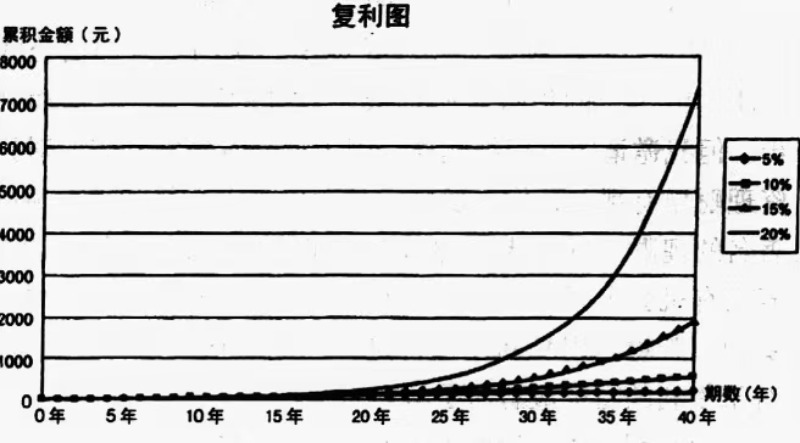
图1-2:不同利率、期数下,1元之年金未来值增长图(40年)
上述两个图形,皆显示在不同利率与期数下,一块钱随着时间增长的情形,而比较这两个图,我们不难发现复利具有两项特色:
- 一、当期数(时间)增加,未来值不断上涨,且上涨的幅度越来越快。这就是所谓几何级数成长。时间够长的话,增长的速度惊人,增长的曲线最终将趋近于直线上升。
- 二、不同的利率所代表的曲线,其上涨的程度有显著的差异。高利率曲线和低利率曲线在经过数十年的复利后,造成极大的差异。
总而言之,理财致富以小钱赚大钱的诀窍,即在于利用“以钱赚钱,利滚利”的复利。而复利的特色有二:其一为时间越长复利效果越显著;其二为报酬率越高复利效果愈佳。将复利特色运用在投资理财上,可得到下列两项结论:
- 一、资金投资在高报酬率标的,如股票及房地产上。因为报酬率越高,复利效果愈好,报酬率低,则复利效果不佳。即资金必须投资在高报酬率的标的上,才能使复利发挥巨大的作用,投资在低报酬的地方,复利的作用不大。
- 二、投资之后,长期持有。时间越长,复利效果越显著。时间不够长的话,复利没什么作用。即投资在高报酬的标的然后长期持有,才能让复利发挥巨大的作用,时间不够长,复利亦无从发挥力量。
附录二 理财致富蓝图#
每个人的年龄、个性、适用税率都不尽相同。因此,每个人需要利用其适合的方式来累积财富。作者没有机会和你面对面,针对你个人的财务需求,设计出适合你的理财规划;亦无法只以几个通用的例子,去涵盖多数人的财务状况与理财计划。
为了协助你规划自己的“理财致富蓝图”,作者结合了财务学中未来值与年金未来值的公式,在此提出一个能适用于每个人与每种财务情况的“投资理财致富公式”。使读者能依照自己的特殊财务情况与理财目标,来规划未来终身的理财大计。
上述公式中复杂计算部分的数值(未来值因子与年金未来值因子),可以查阅本书的附录一得知。
未来值因子:当利率(或报酬率)等于R%时,现在的1元,在第N年后的未来值。 年金未来值因子:当利率(或报酬率)等于R%时,每年年底固定存1元的年金,在第N年后的未来值。
有了上述的公式,读者只要计算出自己目前有多少财产、每年平均可以存下来供理财的金额、预计累积财富的年限以及每年预期可以达到的平均投资报酬率,未来财富的水准都可以利用计算或查表得知。
上述公式是实际情况的简化,因为未来的投资报酬率,不太可能每年维持在固定的水准,且每年存入的资金亦不尽相同。不过,大体而言,利用未来每年“平均”报酬率与“平均”的投入金额,带入公式所求得的未来财富,和实际的情况相差不会太大。
提出“投资理财致富公式”的目的,并不是帮助读者求出未来财富的精确值,而是要投资人了解,投资如何能增加财富及说明理财何以能致富,进而坚定读者理财的信心,方能在漫长而动荡的过程中,抓住理财重点,保持恒心与毅力,稳步地迈向投资致富之道。
这不是万无一失的致富公式,依照这套方法去做,可能使你顺利地成为亿万富翁,但也可能失败;但是如果不做,则致富的机会等于零。理财致富的观念最有价值的地方是告诉你:“投资理财可以致富”有了这种认知至少让你乐观、充满希望。不管你现在拥有多少财富、今年几岁、一年能省下多少钱、投资理财的能力如何,只要你愿意,有决心,愿意学习理财,都能利用投资来增加财富。
读者在了解上述的公式后,可依循下列的步骤,来进行投资理财的事前规划。其步骤如下:
一、基本资料收集:
- 你目前所拥有的资产总额是多少?包括银行存款、股票、房地产等等。
- 你未来每年预计能省下多少钱以供投资?
- 你未来管理资产的平均投资报酬率?
- 你计划几年后达到理财目标?
- 你未来的财富目标?
二、试算
- 你可以根据以上的五项资料,带入“投资理财致富公式”,查看你的财富计划是否可行?若不可行,你将如何应对?是加强储蓄,以增加每年能省下的金额?是学习投资,以提高投资报酬率?是降低自己未来的财富目标?还是延后达到目标的时间?改变其中的变数之后,再带入公式计算。如此反复试算,直到找出一个适于自己且确实可行的投资理财计划为止。
- 你可以根据现有资产、预计完成目标的年数、每年预计可以省下的金额与投资报酬率,来推算你到时能累积的财富有多少。
- 你也可以根据现有财富、完成目标年数、每年省下的金额、投资报酬率、财富目标等五项变数中的任何四项,去求另一项变数。(如果利用其他四项变数去求完成目标年数或投资报酬率,无法直接求出。除非有财务用计算机,否则只能利用试算法,找出近似值。)
“投资理财致富公式”虽然附有看似复杂的数学公式,但我们主要的目的,是运用它来说明投资致富的原理,而不是以它来增加理财的复杂性,也不想因它而困扰读者。因此,手边没有计算机或者是不想大费周章了解或计算公式的人,大可忽略这个公式,不必担心如何计算与如何使用。
会运用“投资理财致富公式”,能够帮助你规划自己未来的财务状况,增强你的理财信心,并不代表就保证能投资致富。理财成功的关键,事前的规划仅是个开端,重点在于是否能掌握投资理财秘诀,并能身体力行。在开始理财时,先弄清自己的财务状况,制定实际可行的财富目标,再根据“投资理财致富公式”评估一下你应该如何投资,需要多久的时间可以完成目标。切记!致富之路操之在己,旁人是无法代劳的。
范例:假设张三目前30岁,身边已有存款20万元,在读完本书后,下定决心,要让自己在这辈子成为亿万富翁,其预计每年可以存10万元,将其投入报酬率20%的股票、房地产上,张三希望能在50岁达到目标,于是采用本书所提供的理财致富公式试算,看看依上述条件能否达到。
根据公式计算得知,张三以现有20万,加上未来20年,每年投入10万于平均报酬率20%的股票、房地产,20年后的财富,约为2600万,不及亿万的三分之一。张三若仍想成为亿万富翁,他可以朝三个方向努力——提高报酬、提高每年投入的金额及拉长完成目标的时间。事实上,20%可算是相当不错的报酬率,仍然合理,纵使投资大师的平均报酬率,顶多也为23%-30%,更何况一般投资人。故提高报酬率较不可能,但张三不考虑拉长致富时间,于是他能做的,便是提高每年投入的金额,于是他更加节俭,且晚上兼差,终于提高每年的投资金额至20万,让我们再为他试算一下,他20年后的财富。
根据公式计算得知,在其他条件不变的情况下,每年投入的金额,增为两倍,20年后的财富,仍不及亿万之半。20%的报酬率、每年投入20万的金额,两者皆已达张三的极限,于是不得不拉长成为亿万富翁的时间,最后他决定将时间拉长至25年,让我们再为他算一算。
果然他终于如愿以偿,能在25年后成为亿万富翁。仅仅将时间拉长5年,便可轻松地成为亿万富翁,若时间再长,他每年所需投入的金额会更少,由这个例子,也可以验证本书中所强调的观念,“年轻就是理财致富的本钱”及“理财是需要长时间才能看出复利效果”,读者可再试试改变其他变数,借以了解究竟哪些较为重要?最后读者必可发现,现有财富及每年投入的金额,影响很小,而时间长短及报酬率才是致富的关键因素。
你的条件也许优于张三许多,也许不及张三,这都无所谓,每个人的条件不一,但一样可以成为亿万富翁,现在马上动手,试算一下,依你现有的条件,要如何才能成为亿万富翁。切记!只要少许的资金,将其投入高报酬的股票、房地产,以及长时间的持有,成为亿万富翁,绝对不是梦。
现在就请你制定你的理财目标,简单的写下你人生理财的目标是多少钱,预计在多少年达到你的目标,以及达到之后,要如何使用财富,来达到人生更高的理想。
切记“金钱是达到人生目标的手段,而不是目标。”
钱不是赚得越多越好,而理财的目标也不是越多越好,若是如此,你将永远达不到目标,况且会使自己因无法达到目标而陷入痛苦、贪婪的深渊,一生不但成为金钱的奴隶,而且留下太多钱来毁掉下一代,对自己、对周围的人、对下一代以及对社会都没有贡献。
有了理财的目标后,接着就依据“理财公式”,试算一下达到理财目标的方法,包括一年该储蓄多少钱、资产平均必须有多少报酬率,由此决定你的资产应以何种方式投资,以及你必须等待多少年,才能实现理财目标。更重要的是,当你达到你的致富目标后,你将如何运用这笔钱。如此能使你的致富梦想更具体化。同时你将发现,只要运用本书所说的理财原则,并持之以恒,将来要成为亿万富翁并非难事。目标明确后,生活将可过得更快乐,乐观的生活态度也会帮助你在工作、做人等方面更成功。
